Anexo: Análisis de supervivencia con edad
Las prevalencias ajustadas del efecto combinado de edad con obesidad, hipertensión y diabetes, suponen que el efecto de la enfermedad es constante para diferentes edades. Este supuesto puede resultar inadecuado para los datos en cuestión. Una forma relajar este supuesto sería crear un conjunto de variables binarias para cada año de edad. Este modelo es equivalente a los modelos de análisis de eventos de tiempo discreto.
\(log(\frac {p_{ti}} {1−p_{ti}})=\alpha D_{ti}+βx_{ti}\)
Donde \(p_{ti}\) es la probabilidad del evento, \(D_{ti}\) es el vector de la duración acumulada (i.e. variables binarias, en este caso una para cada edad individual) y \(x_{ti}\) son las variables de ajuste del modelo. Se puede apreciar que este modelo es un caso especial de un modelo logístico utilizado para producir las probabildiades ajustadas donde la edad interactua, aunque de manera constante, con las \(x_i\)’s.
Este modelo es estimable con estadística bayesiana, sin embargo, el modelo tardaría varias horas en converger.
Una ventaja de la estadística clásica (o frecuentista) es que los modelos de supervivencia tienen una aplicación bastante estandarizada y mucho más veloz. Estos modelos -tal y como los modelos para tiempos discretos- consideran el efecto (no lineal) que el tiempo, como la edad, tiene sobre la probabilidad de experimentar cierto evento, en este caso el fallecimiento por COVID-19. Estos modelos toman la forma:
\(h_i(t)=h_0(t) exp(βx_i)\)
donde \(h_i(t)\) es el riesgo de fallecer por COVID-19 para una persona en el timepo \(t\) (o en este caso la edad) y \(h_0(t)\) es el riesgo de base, i.e. cuando \(x_i=0\).
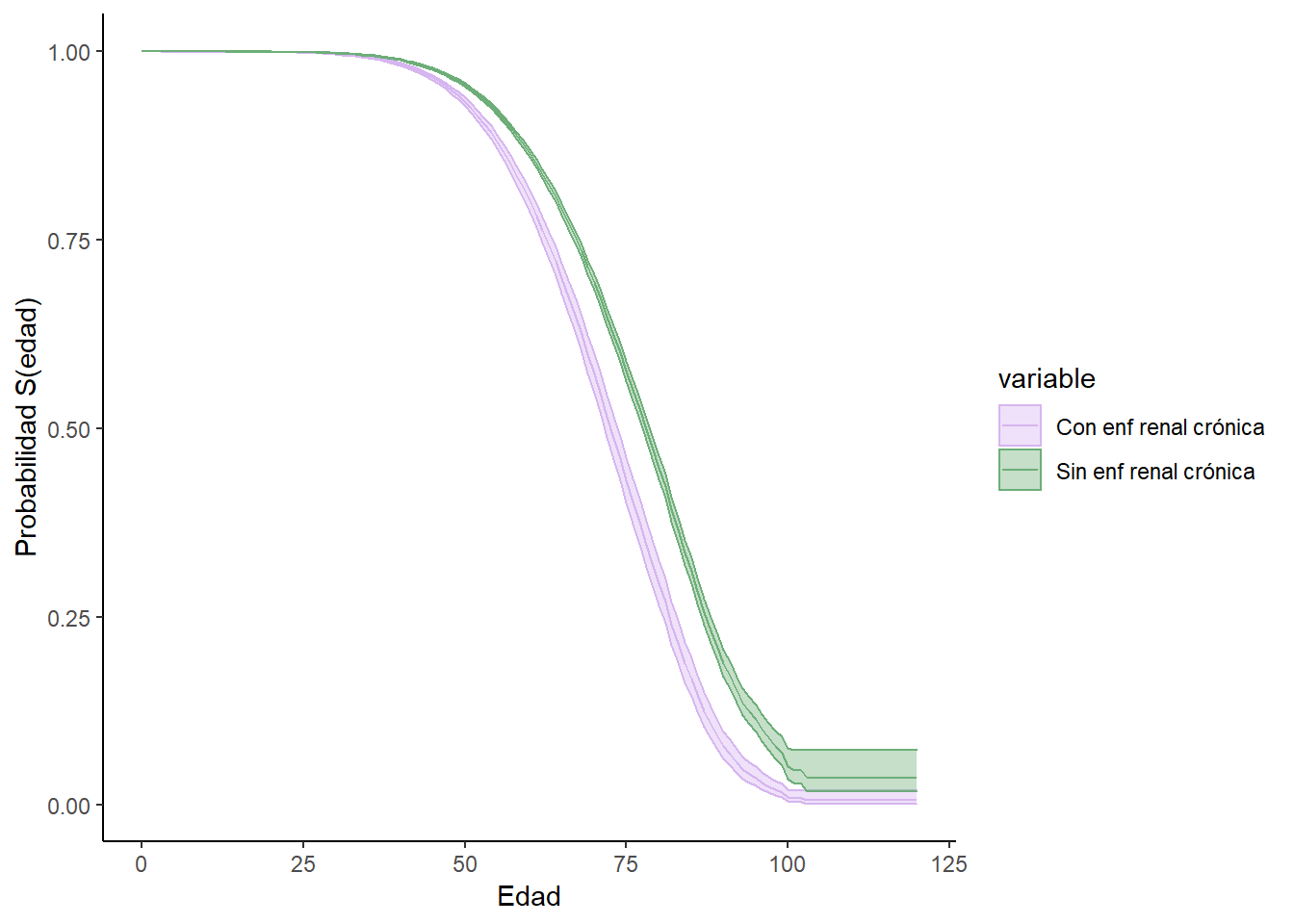
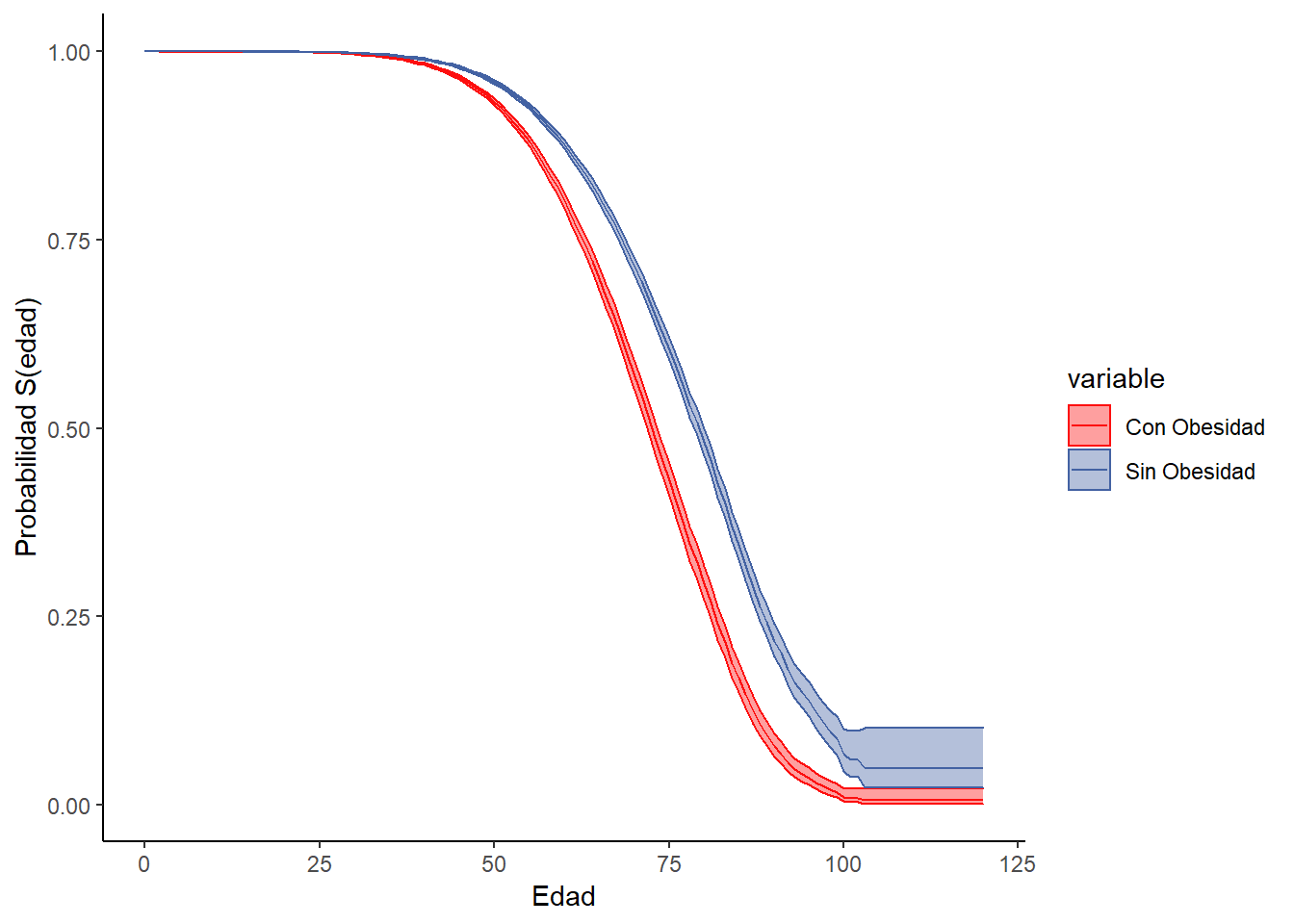
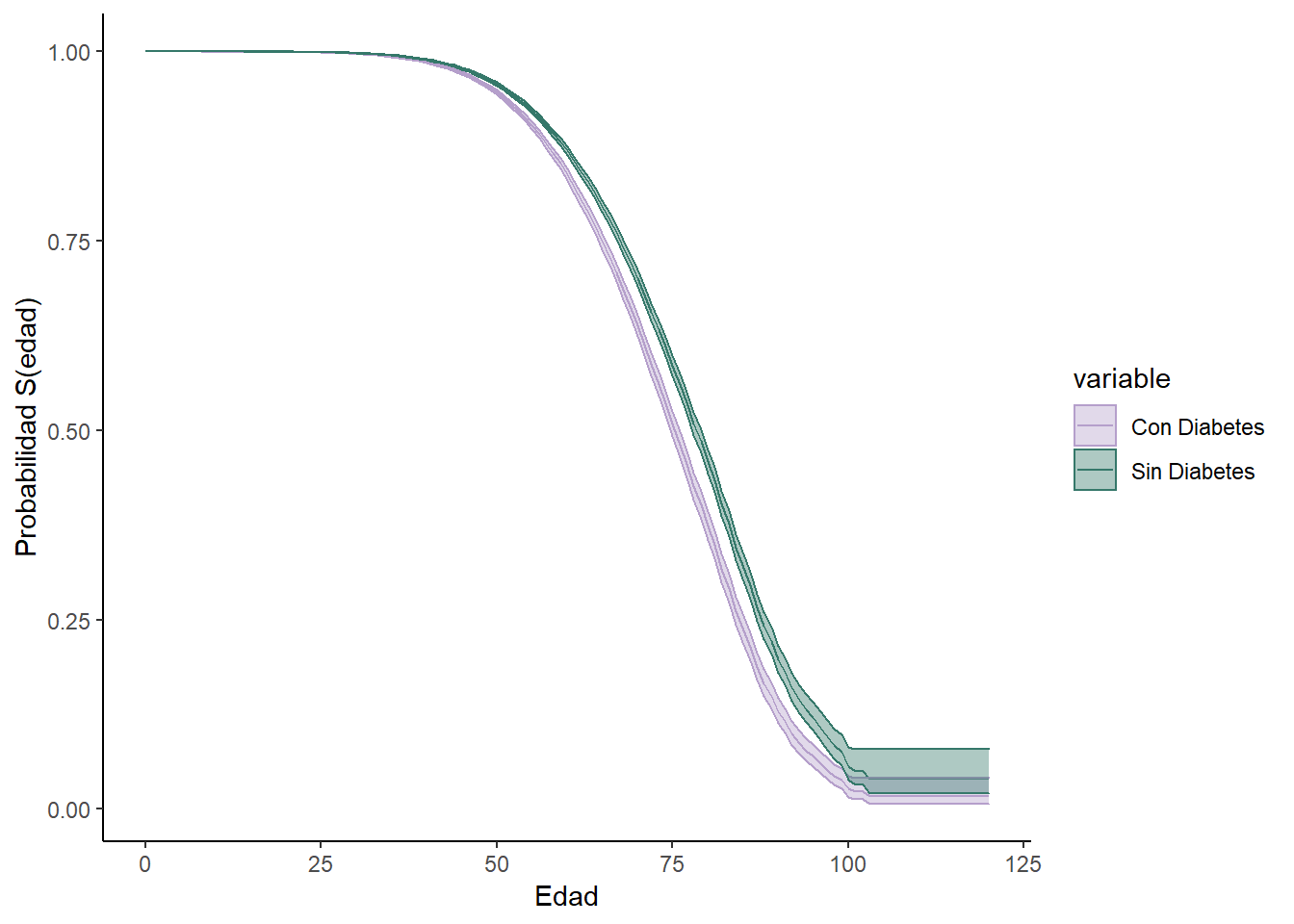
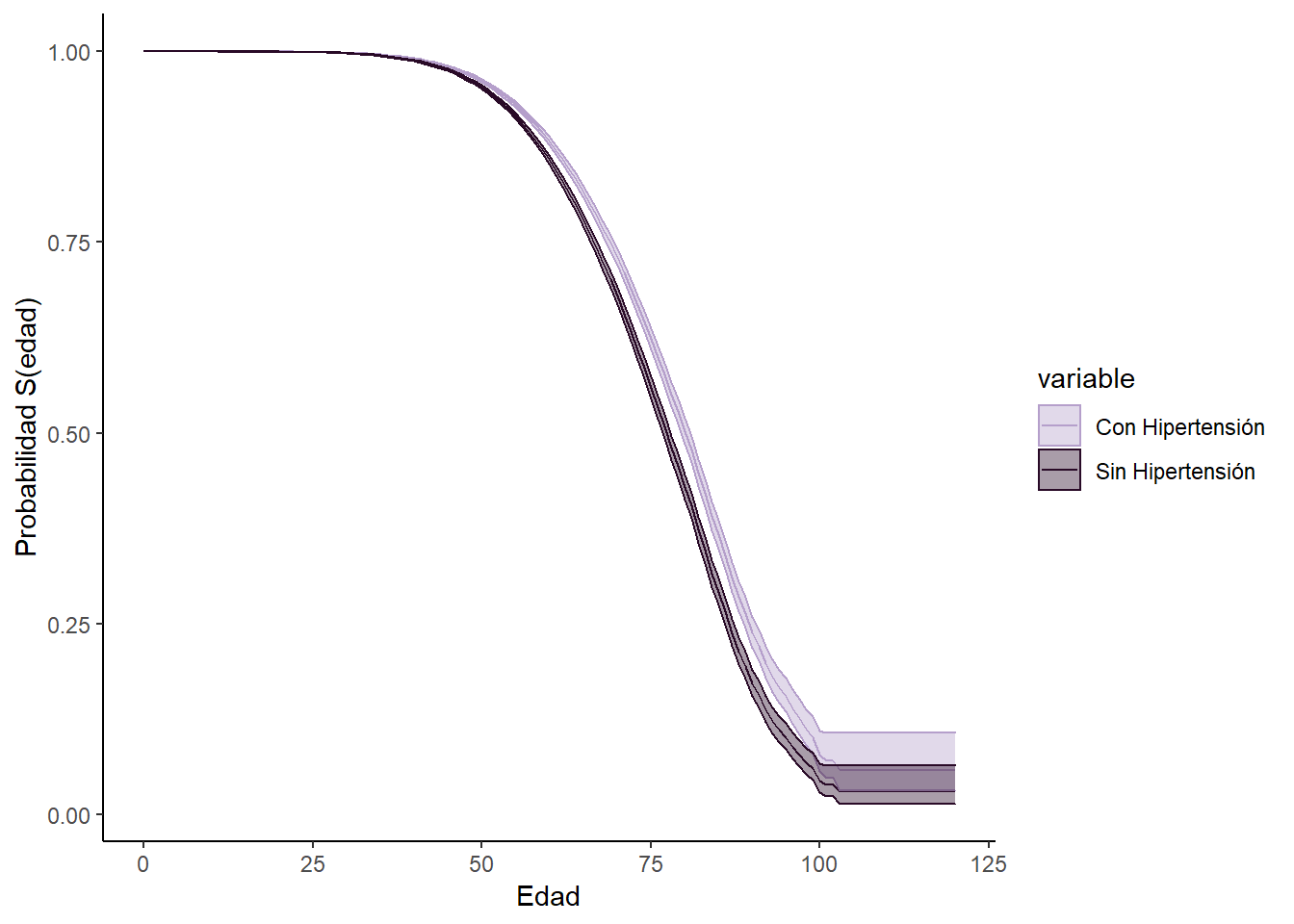
Con el fin de examinar de manera menos conservadora al efecto de la edad, se estimaron modelos de supervivencia (continuos -Regresión de Cox- y discretos -modelos logísticos con interacciones-) a los datos hospitalarios de la SSA. Los modelos ajustan por las mismas variables que el modelo bayesiano. A continuación, se presentan las curvas de sobrevivencia del modelo de regresión de Cox -los resultados son similares al de tiempo discreto y se omiten para evitar redundancias-, en el que la probabilidad de fallecer es función de la edad -considerando los otros factores a sus valores muestrales promedio-.
Estimaciones modelos de análisis de sobrevivencia
Obesidad
Diabetes
Hipertension
Renal crónica